KUKA youBot Mobile Manipulation
In this project, I developed a full trajectory planning and control pipeline for the youBot mobile manipulator using Modern Robotics. The robot had to autonomously pick up a block from an initial position and drop it off at a final location in CoppeliaSim, with accurate grasping and movement under a physics engine.
The system plans and follows a reference trajectory for the end-effector using kinematic simulation and feedback control. The output is a CSV file containing the robot’s full configuration (chassis pose, arm joints, wheel angles, gripper state) over time, which is used to animate and test the robot in CoppeliaSim’s physics-based Scene 6.
DEMO

ALGORITHM DESCRIPTION
The system includes three main modules:
NextState: Simulates the next robot configuration based on the current configuration and commanded speeds using Euler integration.TrajectoryGenerator: Builds the reference trajectory for the end-effector in task space, including 8 motion segments with associated gripper states.FeedbackControl: Computes the end-effector twist command based on the error between the current and desired configurations using a feedforward plus proportional-integral (PI) controller.
TRAJECTORY GENERATOR
The TrajectoryGenerator creates eight concatenated trajectory segments in SE(3), each starting and ending at rest:
- Move to standoff above initial block.
- Lower to grasp pose.
- Close gripper.
- Lift to standoff.
- Move to standoff above goal.
- Lower to place pose.
- Open gripper.
- Return to standoff.
Each segment includes both rotational and translational interpolation, with 0.01s resolution.
INITIAL SETUP
The initial end-effector pose is purposely offset by:
- 0.2 m translation in the X-axis
- 30° rotation about the Z-axis
This ensures a meaningful starting error that the feedback controller must reduce over time.
The initial configuration vector for the robot is:
[chassis φ, x, y, J1-J5, W1-W4, gripper state]
FEEDFORWARD CONTROL
The computed twist is mapped to wheel and joint velocities using the robot Jacobian:
- The base Jacobian is derived using wheel geometry and screw theory.
- The arm Jacobian is computed via
JacobianBody.
The combined Jacobian maps the desired twist to joint and wheel speeds using the pseudo-inverse.
Velocity saturation ensures the commanded speeds stay within physical actuator limits.
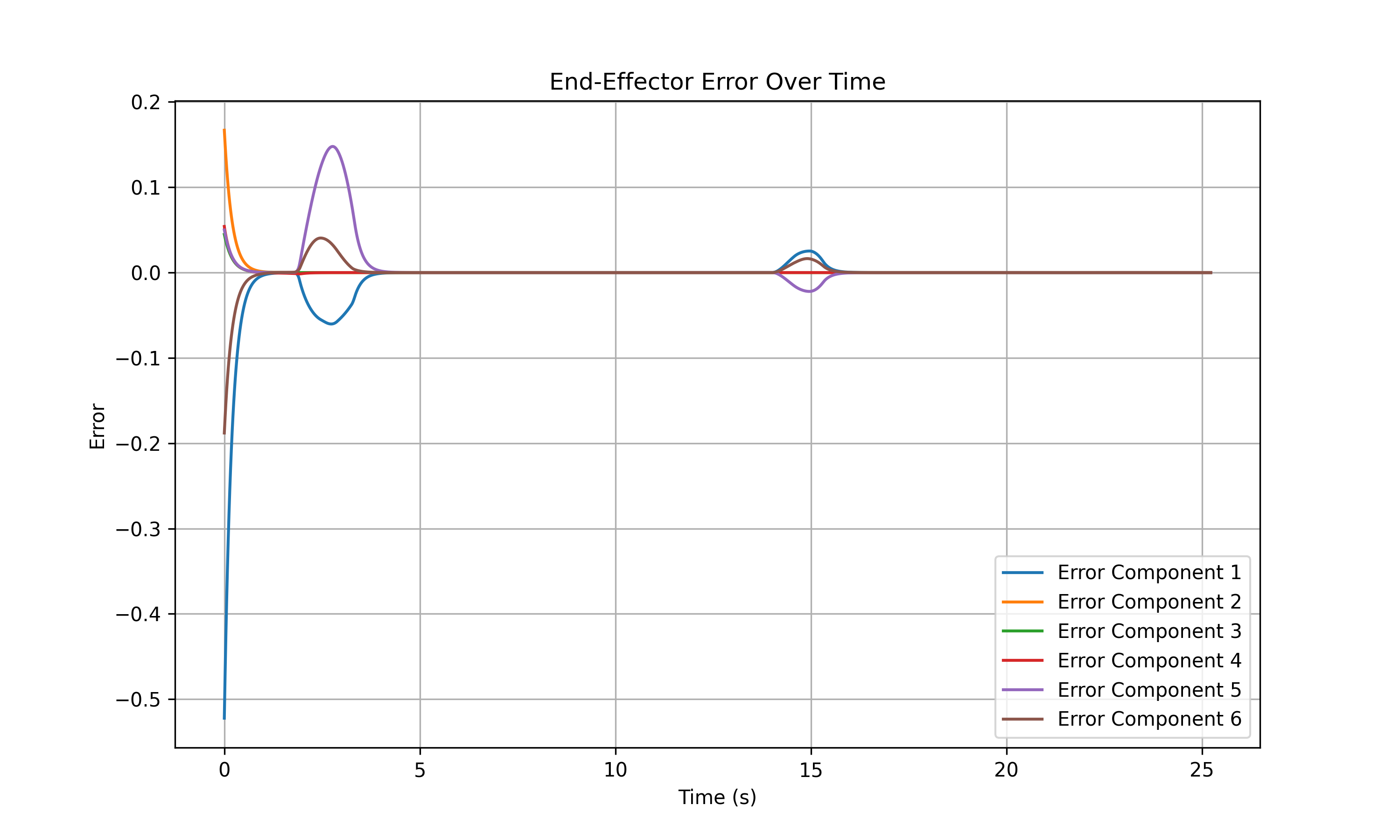
RESULTS
BEST CASE
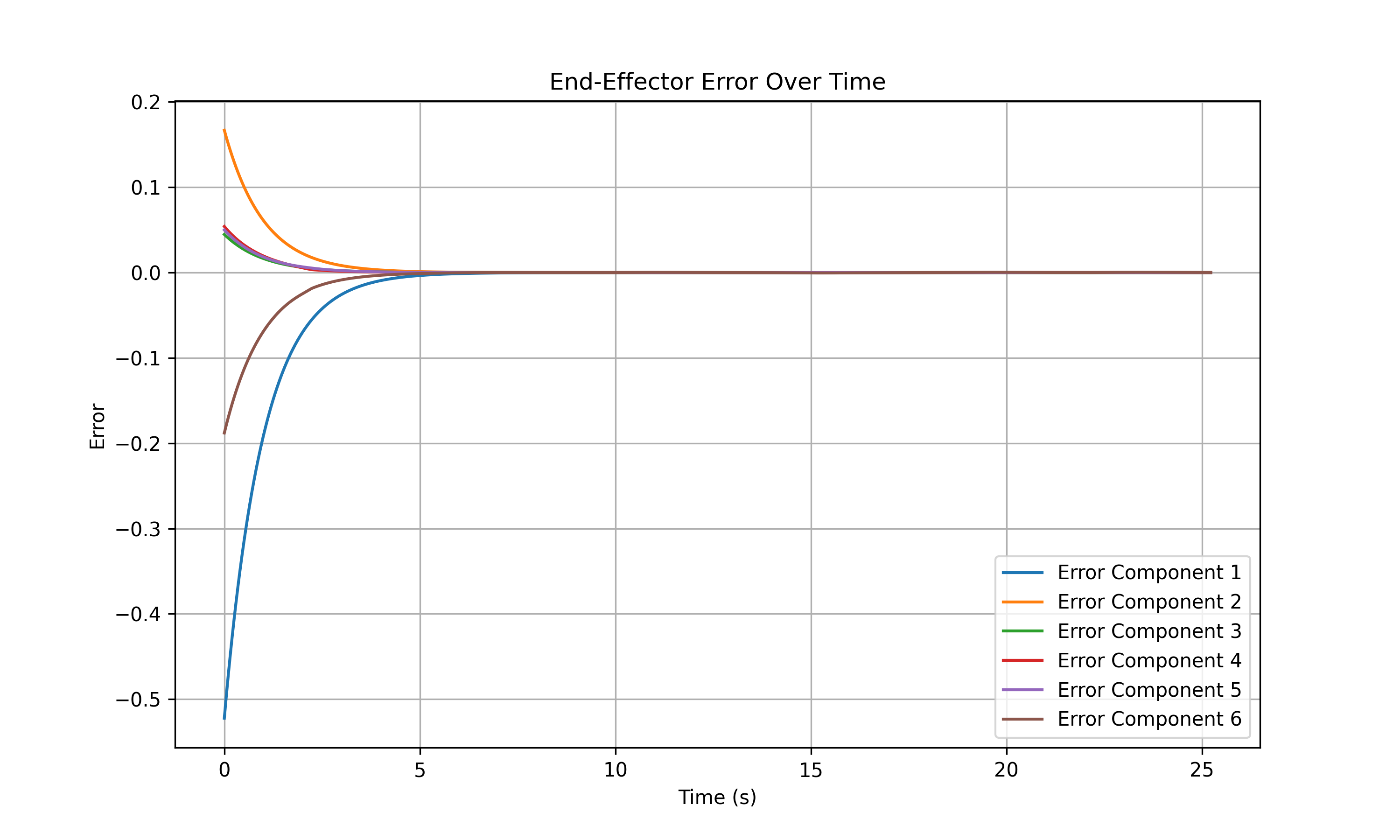
OVERSHOOT CASE
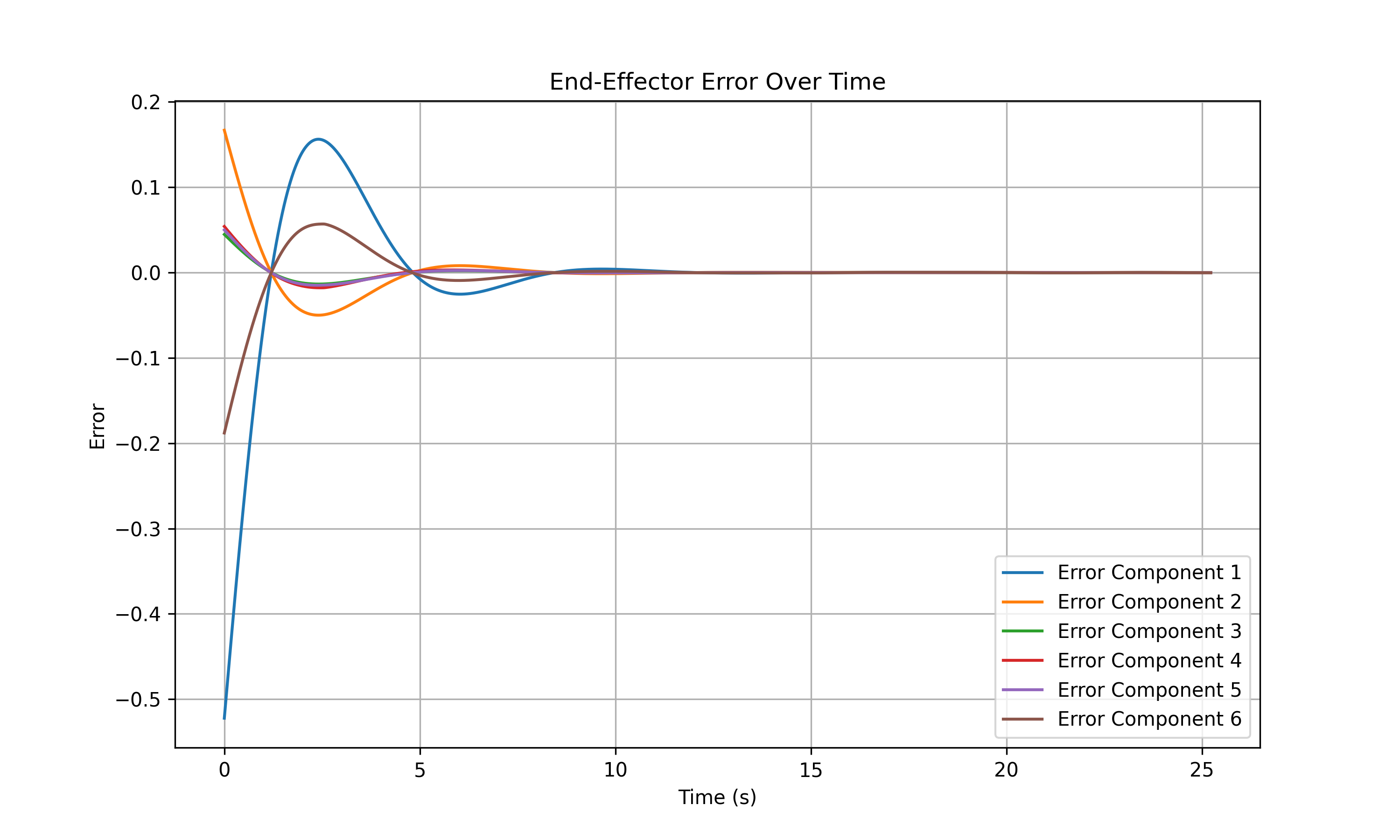
NEW TASK